
DICE of the GODS


To create the "Dice of the Gods", otherwise known as the five platonic solids: tetrahedron, octahedron, cube, icosahedron, and dodecahedron, you will need:
- several greeting cards or pieces of colored card stock or even cereal box sides
- a compass for drawing circles
- a ball point pen
- a ruler or straightedge
- a pair of scissors
- a stapler or glue if you prefer


You are going to need to inscribe an equilateral (all sides the same length) triangle inside the circle.
To do this, keep the compass locked open to the same radius you used above and draw a single starting point on the circle.
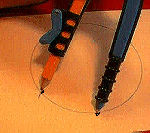


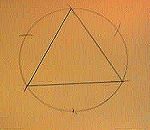
Now connect every other mark with your straight edge and you will have created an inscribed equilateral triangle into the circle.
*We will be using the circle pattern first, and then we will cut out the triangle and use it as a pattern.





You will need to cut out a circle for each face, or side, of the polyhedron you are making.
- tetrahedron = 4 circles
- octahedron = 8 circles
- cube = 6 circles*
- icosahderon = 20 circles
- dodecahedron = 12 circles**
* The cube will need to have a square inscribed into each circle instead of a triangle.
** The dodecahedron will need to have a regular pentagon inscribed into each circle.



RED ALERT: this step is vital!
Be sure to use your straight edge and the ball point pen to go over very firmly each side of this triangle you just traced.
This is known as "scoring" and it will give you a perfect fold, because the pressure of the pen starts the crease of your fold.

All you will need to do is lightly press the scored flaps up.
*NOTE: if you fold them up as in this demonstration, your polyhedron will be quite decorative with the flaps showing on the outside.

If you would rather have a smooth outer skin with no flaps showing, we recommend folding them down and using glue instead of staples to attach the flaps.


We are going to make the above icosahedron. So start stapling flaps. Usually one or two staples placed close to the fold line will do the trick.
If you want a firmer, more rigid bond, we recommend white glue. Remember however that this will greatly increase your construction time, as you will have to wait for the glue to dry.





Here is the finished product. Click the image for a larger view.
Please note that all of the platonic solids can be made in this manner.
Click HERE if you want to see the patterns for the others.
 Cut
and Assemble 3-D Geometrical Shapes...
Cut
and Assemble 3-D Geometrical Shapes...
We highly recommend
this cut and assemble book. These figures are sturdy and very brightly
colored. They will last for years and rotate gracefully when hung from
a ceiling. Usually ships in 24 hours.
Home | About
Us | Algebra| Dictionary | Games | Geometry | Gym | Humor | Lab | Magic | Natural Math | PreAlgebra | Resources | Teachers Only | Toolbox | Treasures | Videos | Wonders | Writings |
Copyright © 1999-2020 themathlab.com
