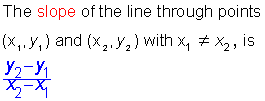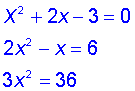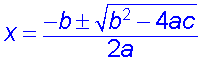Geometry
Legal Reasons |
|
Algebra
and General Math
Master List of Legal Reasons How to Play | Game Levels | Reasons | Cards | Game Board | Writing Proofs |
| General Math Legal Reasons: | ||
| 1 | Definition of Prime Number | A prime number is an integer, other than zero or one, that has only two factors, itself and one. |
| 2 | Definition of Even Number | An even number is an integer which is divisible by two. All even numbers can be written in the form 2n, where n is an integer. |
| 3 | Definition of Odd Number | An odd number is an integer which is not divisible by two. All odd numbers can be weritten in the form 2n + 1 or 2n - 1, where n is an integer. |
| 4 | Definition of Radius of a Circle | The radius of a circle is the distance from the center of the circle to any point on the circle. |
| 5 | Definition of the Diameter of a Circle | The diameter of a circle is equal to two times the radius, (d=2r). |
| Algebra Legal Reasons: | |||
| 1 | Definition of Set of Natural Numbers | Counting numbers beginning at one and continuing infinitely {1, 2, 3, 4,...} | |
| 2 | Definition of Set of Whole Numbers | Set of Natural
Numbers and zero {0, 1, 2, 3, 4,...} |
|
| 3 | Definition of Set of Integers | Set of Whole
Numbers and their opposites {...-3, -2, -1, 0, 1, 2, 3,...} |
|
| 4 | Definition of Set of Rational Numbers | All numbers which can be written as a quotient of integers including all integers, fractions, mixed numbers, terminating decimals, and repeating decimals. | |
| 5 | Definition of Set of Irrational Numbers | All numbers which cannot be written as a quotient of integers, including all square roots of non perfect squares, and all non repeating, non terminating decimals. | |
| 6 | Definition of Set of Real Numbers | All Rational and Irrational Numbers. | |
| 7 | Addition, Subtraction, Multiplication, and Division of Real Numbers | All correct use of these operations done on the set of Real Numbers will result in an answer in the set of Real Numbers and can be used as a legal reason in a geometric proof. Simply state for example: "Addition fact, over the set of Real Numbers." | |
| 8 | Definition of Exponents |
y^n = y * y * y *
y... 'n' times. |
|
| 9 | Definition of Absolute Value | The absolute
value of a number is the positive distance that the number is
from zero. Zero has an absolute value of zero. |a| = a if a >= 0 & -a if a < 0 EX: |-3| = 3 EX: |14| = 14 EX: |-3 + 4| = 1 *Note: always simplify inside the absolute value bars before making the number positive. |
|
| 10 | Commutative Property of +, x | For all
a,b,c elements of the Reals, a + b + c = b + a + c a * b * c = c * a * b In other words, you can change the order of the numbers when multiplying or adding, and your answer remains the same. |
|
| 11 | Associative Property of +, x | For all a,b,c
elements of the Reals, (a + b) + c = a + (b + c) (a * b) * c = a * (b * c) Here, the only things that change are the grouping symbols. Once again, the answers remain the same, regardless of which group gets added or multiplied first. |
|
| 12 | Distributive Property of Multiplication | For all a,b,c
elements of the Reals, a(b + c) = ab + ac a(b - c) = ab - ac Remember, when multiplying a number times a GROUP, always multiply by everything INSIDE that group. |
|
| 13 | Addition Property of Equality and Inequality |
For all a,b,c
elements of the Reals, |
|
| 14 | Subtraction Property of Equality | For
all a,b,c elements of the Reals, if a = b, then a - c = b - c. In order to maintain balance, whatever number you subtract from one side of an equation must be subtracted from the other side also. |
|
| 15 | Multiplication Property of Equality and Inequality |
For all a,b,c
elements of the Reals, |
|
| 16 | Division Property of Equality | For
all a,b,c,elements of the Reals, where
c is NOT equal to zero, if a = b, then a/c = b/c. To maintain the balance of the equation, you must always remember to divide BOTH sides of the equation by the same number. |
|
| 17 | Property of Opposites | For
every a element of the Reals, a + -a = 0 |
|
| 18 | Property of Inverses | For every
b element of the Reals, b * 1/b = 1 |
|
| 19 | Additive Identity | For all x
element of the Reals, x + 0 = x ZERO is the only number that you can add to any other number without changing the other number's identity. That is how it gets its name as the "additive identity". |
|
| 20 | Multiplicative Identity | For all x
element of the Reals, x * 1 = x ONE is the only number you can multiply by any other number and not change the identity of the other number. Therefore ONE is known as the multiplicative identity. |
|
| 21 | Substitution Principle | If one value is equivalent to another value, the two can be substituted for each other in mathematical statements. | |
| 22 | Definition of Slope |
When a linear equation is written in "slope intercept form" it is solved for y and looks like this: y = mx + b. The number "m", in front of the x, is the slope, or steepness of the line. The number in the "b" spot is the y intercept, the place where the line crosses the y axis.
|
|
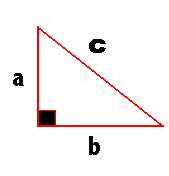
| 23 | Pythagorean Theorem |
Given any right triangle with legs a and b and hypotenuse c the following relationship holds:
|
|
| 24 | Quadratic Formula |
A quadratic equation
in x is an equation involving x to the power 2 but no higher powers
of x. The STANDARD FORM
of a quadratic equation is, |
|
|
How to Play | Game Levels | Reasons | Cards | Game Board | Writing Proofs
Copyright © 1999-2020 themathlab.com  |
|||