Math "I" Terms

Mathematical "I" Words
*Dictionary Alert

icosahedron A polyhedron with twenty faces.

identity transformation A transformation that maps each point onto itself.

if and only if statement A statement consisting of a conditional and its converse. Also called biconditional.

EX:
A quadrilateral is a square if and only if it is a rhombus and a rectangle.

NOTE: The if and only if part , sometimes abbreviated as iff, guarantees that the statement can be read as an "if then" statement from front to back and from back to front, known as the converse. This is how the above example would read in both directions:

Front to back: If a quadrilateral is a square, then it is a rhombus and a rectangle.

Back to front: If a quadrilateral is a rhombus and a rectangle, then it is a square.

if-then statement A statement of the form If... Then....
Ex:
If a quadrilateral has four equal sides then it is a rhombus.

image The result of applying a transformation to an original figure or preimage. Transformations can be reflections, as seen in the example below, rotations, translations or "slides", and glide reflections.
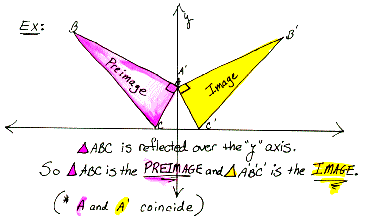
Images come from either reflecting, rotating, translating, or glide reflecting.

image point A point resulting from applying a transformation. In the example above, C', read "C prime", is the image point of preimage point C.

impossible event An event with a probability of 0 .

inch ( in) The base unit of length for the US system of measurement.
1 in is exactly equal to 2.54 centimeters.

included angle The angle formed by two consecutive sides of a polygon.

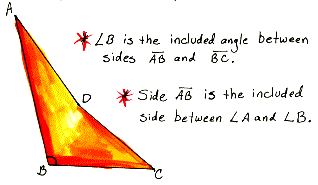
included side The side between two consecutive angles of a polygon.

indirect reasoning (proofs) Reasoning (proofs) using the Law of the Contrapositive, the Law of Ruling Out Possibilities, or the Law of Indirect Reasoning.

inequality A sentence with one of the following symbols:

<(less than),
>(greater than),
<(less than or equal to),
>(greater than or equal to).

infinite decimal A decimal that goes on forever to the right of the decimal point. Some of these decimals repeat and some do not. The ones which do not are called irrational numbers examples of which are pi and the square root of two.

infinite repeating decimal A decimal in which a digit or group of digits to the right of the decimal point repeats forever.
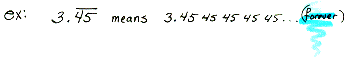
The numbers under the bar are known as the "repetend".

initial point The beginning point of a vector.

inscribed angle in a circle An angle whose vertex is on the circle and whose sides each intersect the circle at a point other than the vertex.

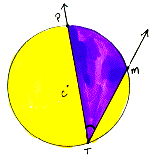Point T is the vertex of this inscribed angle

Angle PTM is an inscribed angle with its vertex point T on the circle C.

Notice both sides cross the circle at points other than T.

inscribed circle In a polygon, a circle which is tangent to, or touches, each side of the polygon.

A circle fit snugly inside of a polygon.

Here we see a circle that fits perfectly inside of a polygon. The circle ever so lightly touches each side of the polygon, but does not go past its edges.

inscribed polygon In a circle, a polygon whose vertices all lie on the circle.

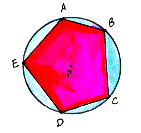A polygon fit snugly inside of a circle.

Notice the difference here. In this case, the polygon is inside the circle with each of its vertices on the circle.

instance An example of a pattern.
EX:
3x+7 is the pattern and 3(1)+7 = 10 is an instance of that pattern.

instance of a conditional A specific case in which the antecedent (if part) of the conditional is true and its consequent (then part) is also true.
EX:
If x is not equal to zero, then x squared is a positive number. An instance here would be let x=(-14), then (-14) squared is equal to 196 which is a positive number.

integer A number which is a positive whole number, a negative whole number, or zero.
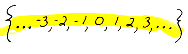
This is an infinite set of numbers. It never ends in either direction.

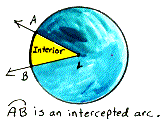
intercepted arc An arc of the circle in the interior of an angle.

interior angles When two lines are cut by a transversal, the angles that are formed on the inside of the two lines are known as interior angles.

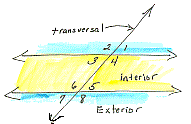In this picture, angles 3, 4, 5, and 6 are all interior angles.

Angles 1, 2, 7, and 8 are called exterior angles.

interior of a circle The set of points at a distance less than the radius from the center of the circle. It's all of the points on the inside of the circle.

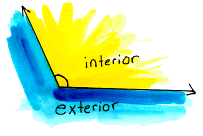
interior of an angle A nonzero angle separates the plane into two sets of points. If the angle is not straight, the convex set is the interior of the angle.
The interior of this angle is yellow.

international system of measurement A system of measurements based on the decimal system. Also called metric system.

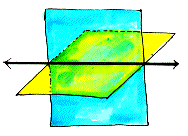
intersecting planes Two planes that contain the same line.
EX:

intersection of two sets The set of elements which are in both the sets.
EX:
Given set A={1, 2, 3, 4} and set B={3, 4, 5, 6},
the intersection of sets A and B, written = {3, 4}.

interval on a scale The constant difference between successive tick marks on the scale of a graph.

inverse A conditional resulting from negating the antecedent and consequent of the original conditional.
EX:

Original conditional: If a quadrilateral is a square, then it is a rectangle.

Inverse: If a quadrilateral is not a square, then it is not a rectangle.

NOTE: Sometimes the original conditional will be true, but its inverse will be false. Be careful with these.

irrational number A number that cannot be written as a simple fraction. It is an infinite and nonrepeating decimal. Examples are "pi" and the square root of two.

isometry A transformation that is a reflection or a composite of reflections. Also called congruence transformation or distance-preserving transformation. Reflections, rotations, translations or slides, and glide reflections are all isometries.

isosceles trapezoid A trapezoid with a pair of non parallel sides the same measure. In an isosceles trapezoid, the base angles will be congruent.
Non parallel sides are congruent.

isosceles triangle A triangle with two sides equal in length.
The third side is called the base.