The Challenge of Creating a

GRACEFUL NETWORK

Here is a puzzle using networks that just might become addicting:

Start with a network that has n arcs. (The networks on the background of this page have four nodes and 6 arcs.)

Name each node with a different number from 0 to n. Then number each arc by the absolute value of the difference of the nodes it connects.

For example, look at the "graceful" network here.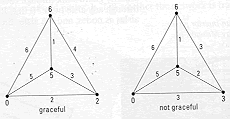

The arc connecting nodes 5 and 2 is named 3 because |5 - 2| = 3.

The goal is to name the nodes in such a way that the n arcs are numbered with all the integers from 1 to n.

If you can do it,...you will have created a Graceful Network .

We at the math lab know that the networks below can indeed be made "graceful".

Give them a shot.

We ranked them in order of difficulty. It will probably take you several tries before you get them all.

....................................

.........A....................B...........................C

HAVE FUN..when you get one it is a real rush!

We just learned this game. We are not sure if every network in the world can be made "graceful".

We would love to have you submit your own original "graceful" networks. Please feel free to help us expand this exploration by sending us your findings.

If we get a few or more, we will start a gallery. Let us know if you want your name posted with your work.

HAVE FUN EXPLORING!